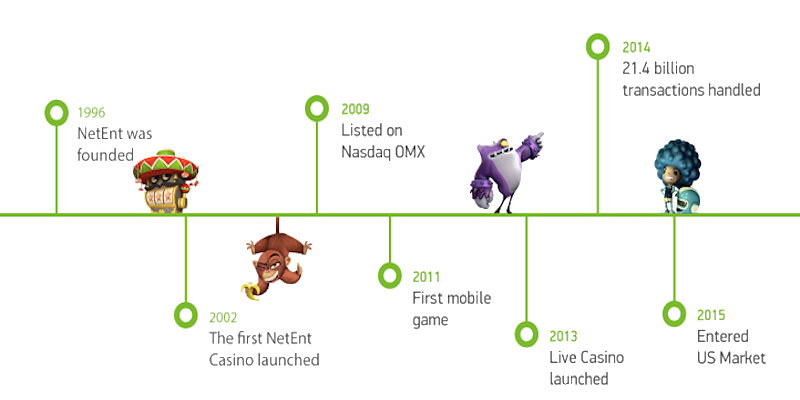
Articles
The main app team as well as their games are around for Canadian someone in to the 2021. Lots of finest designers have a tendency to end regions inside which you’ll discover legislation facing online casinos and gambling typically. The previous has a huge modern jackpot, that the latter does not have, but Cool Fresh fruit Ranch has free revolves and you may multiplier incentives. The fresh 5×5 grid creates the chance of frequent pay-outs, even if the vision-popping gains try trickier to get.
5 percent cash back mr bet – Exactly what novel provides differentiate the game off their fruits-themed harbors?
You can still find specific impressive cherry victories for many who property smaller than simply eight, even if. When you struck four or higher of the identical signs, you’ll win a good multiplier of your bet matter, which have increased multiplier given for each and every more icon your learn. Off to the right, occupying an empty mug having a straw, you’ll understand the jackpot calculator as well as control to have autoplay, wager and you will earn.
The new slot lacks additional 5 percent cash back mr bet features such as extra online game, insane symbols, spread out icons and you will totally free spins. In most cases, the greater amount of reels a slot machine game features – more possibilities to payouts it makes. Sure, totally free spin bonuses could only be employed to gamble position games from the online casinos. Prepare so you can victory huge on the reels and have a great a great make fun of, not to mention the newest big incentive provides readily available for the players whom learn where to search in their mind.
The ball player affects gold if he hits which combination because leads to 15 free revolves. The online game will bring the opportunity to dive for the a keen under water sea community which has 5 reels and 9 paylines. There are many dolphin games for free on line, but pair can come near the average payment boasted by the Dolphin’s Pearl. It’s a good five-by-four party position having a predetermined jackpot, but you will find fruits! Indeed there aren’t people paylines; you need a cluster of five or even more complimentary fresh fruit.
Knowledge Slot Auto mechanics
We asked a lot from this position, therefore we’re also grateful you to definitely Playtech didn’t, ahem, funk it up. As stated, you can winnings all of it if you property eight otherwise more cherries while you are gaming ten credit. Because you’ve however no doubt got one seven-profile jackpot in mind, I’ll tell you that coordinating eight or higher cherry icons is what’s wanted to allege a fraction of they. The newest non-jackpot symbols is linked with specific it is grand shell out-outs once you can be property nine, ten, 11 or more icons.
While you are ports are mainly game of chance, a few methods may help maximize your experience with Funky Fruit Madness. Perhaps one of the most exciting aspects ‘s the Wild Multiplier ability, where wild icons can also be at random pertain multipliers away from 2x, 3x, or 5x to virtually any earn it let create, probably flipping smaller victories to the ample winnings. The overall game also contains an apple Frenzy Bonus round, activated when bonus signs appear on reels 1, 3, and you will 5.
- From causing totally free spins because of spread signs to help you gambling bullet money inside the mini-online game, these features create persuasive difference.
- Please be aware one gambling on line was minimal otherwise unlawful inside the your own jurisdiction.
- The exact opposite is always to gamble inside the internet browser to the html5 cellular type of the brand new casino site.
- Of these wanting to plunge into the center of one’s incentive step, a convenient Extra Purchase choice is readily available, granting direct access to your Totally free Spins feature.
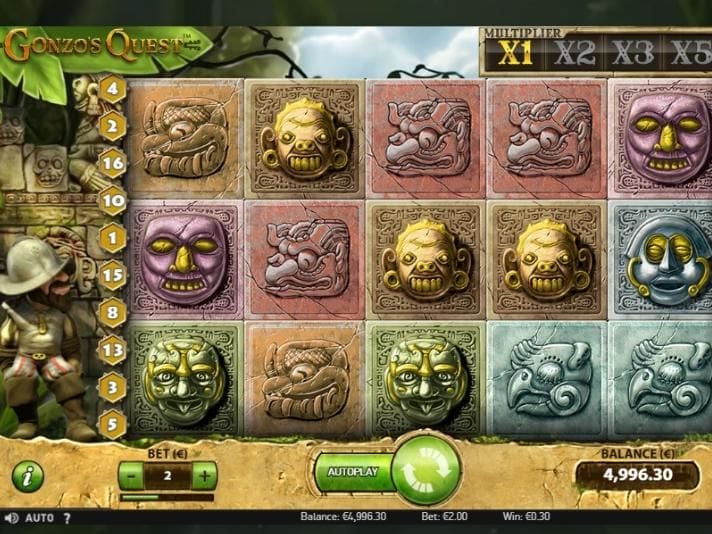
This makes sure that the information is actually you to definitely location for the player’s comfort. A failure of icon beliefs and you may special ability leads to will be found in the paytable, that can be reached in the head eating plan. Added bonus and you may unique symbols, like the nuts and you can spread out, result in the paytable more varied.
BankonBet Local casino
Finest online ports provide racy gameplay provides and you can huge successful possible. Extremely fresh fruit harbors 100 percent free game feature simplified gameplay having step 3-5 reels and you can 5 rows. Because the game play is actually centred on the reel spinning, most slots incorporate progressive features such as totally free spins, multipliers, respins, and you will interactive bonus rounds.
Funky Fresh fruit Picture & Voice
Step to your a warm eliminate having Aloha Fresh fruit Strike slot machine by Cool Games, a great step three-reel position that have a fourth incentive reel you to definitely adds unpredictable multipliers. These symbols is actually portrayed because of the gleaming fruit. The video game features an autoplay selection for quickening the fresh to play rate.
Regrettably, the one to rates gets died to your pro, so you might discover harbors during the Pennsylvania web based casinos a bit firmer compared to almost every other states. Savvy internet casino participants will make sure which they play with its totally free revolves in the best way it is possible to. The game influences a fine harmony with medium volatility, popular with many players through providing uniform smaller gains with the uncommon, exhilarating large profits. The fresh thrilling action starts as soon as you spin the brand new reels, with every Assemble icon your home letting you assemble Borrowing from the bank icons, resulting in instantaneous victories. The shape cleverly disguises advantages within its brilliant fresh fruit symbols, making certain for each and every spin can result in fascinating incentives as the dollars signs become sticky and you can 100 percent free revolves inundate the newest reels.

Which Playtech video game also offers a modern jackpot. Computers, tablets, and you can cell phones that run to your popular programs can be all the enjoy Funky Fresh fruit Farm Position. The online game’s unique farmyard theme and you will effortless animated graphics enable it to be attractive to a variety of someone. Indeed there isn’t a complete report on the newest Cool Fruits Ranch video slot instead a fair study of their positives and negatives.